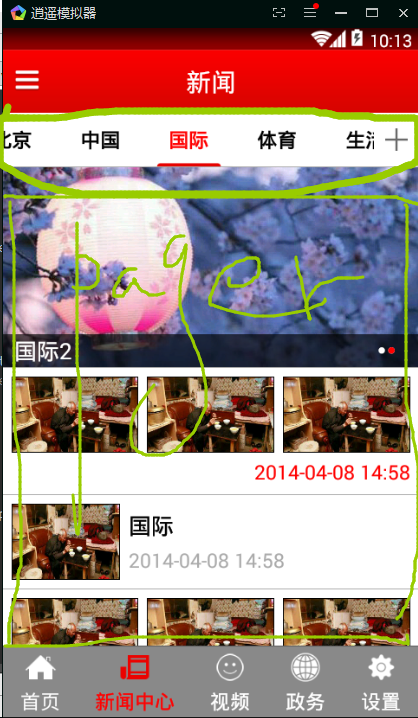
TabPagerIndicator使用
本文共 1433 字,大约阅读时间需要 4 分钟。
 1 注意/在清单文件中配置activity/theme=
1 注意/在清单文件中配置activity/theme=
android:theme="@style/Theme.PageIndicatorDefaults">
// 2 (adpter中添加getPageTitle)
2 (adpter中添加getPageTitle)
//1.给viewPager设置数据适配器 MyPagerAdapter myPagerAdapter = new MyPagerAdapter(); pager.setAdapter(myPagerAdapter); //2.指示器和viewPager进行绑定 indicator.setViewPager(pager);
3 重点(修改选中文字的颜色,背景) values/style/tabPageIndicator
values/style/tabPageIndicator
@android:color/transparent 为加背景,,不能用@null
<item name="vpiTabPageIndicatorStyle">@style/Widget.TabPageIndicator</item>//这里
</style>
<style name="Widget"> </style> <style name="Widget.TabPageIndicator" parent="Widget"> <item name="android:gravity">center</item><item name="android:background">@drawable/vpi__tab_indicator</item>//背景
<item name="android:paddingLeft">22dip</item> <item name="android:paddingRight">22dip</item> <item name="android:paddingTop">12dp</item> <item name="android:paddingBottom">12dp</item> <item name="android:textAppearance">@style/TextAppearance.TabPageIndicator</item> <item name="android:textSize">12sp</item> <item name="android:maxLines">1</item> </style> <style name="TextAppearance.TabPageIndicator" parent="Widget"> <item name="android:textStyle">bold</item><item name="android:textColor">@color/vpi__dark_theme</item>//文字颜色
</style> <style name="Widget.IconPageIndicator" parent="Widget"> <item name="android:layout_marginLeft">6dp</item> <item name="android:layout_marginRight">6dp</item> </style></resources>
你可能感兴趣的文章
MySQL底层概述—8.JOIN排序索引优化
查看>>
MySQL底层概述—9.ACID与事务
查看>>
Mysql建立中英文全文索引(mysql5.7以上)
查看>>
Mysql当前列的值等于上一行的值累加前一列的值
查看>>
MySQL当查询的时候有多个结果,但需要返回一条的情况用GROUP_CONCAT拼接
查看>>
MySQL必知必会(组合Where子句,Not和In操作符)
查看>>
MySQL必知必会总结笔记
查看>>
MySQL快速入门
查看>>
MySQL快速入门——库的操作
查看>>
mysql快速复制一张表的内容,并添加新内容到另一张表中
查看>>
mysql快速查询表的结构和注释,字段等信息
查看>>
mysql怎么删除临时表里的数据_MySQL中关于临时表的一些基本使用方法
查看>>
mysql性能优化
查看>>
MySQL性能优化必备25条
查看>>
Mysql性能优化(1):SQL的执行过程
查看>>
Mysql性能优化(2):数据库索引
查看>>
Mysql性能优化(3):分析执行计划
查看>>
Mysql性能优化(4):优化的注意事项
查看>>
Mysql性能优化(6):读写分离
查看>>
MySQL性能测试及调优中的死锁处理方法
查看>>